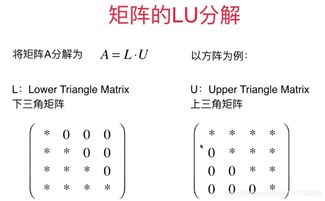
在数学与工程领域，线性系统是描述变量间线性关系的基本模型，而矩阵的逆则是解决这类系统的关键工具。本章将深入探讨线性系统与矩阵逆之间的紧密联系，揭示矩阵系统在理论和应用中的核心地位。

线性系统通常表示为形如 \( Ax = b \) 的矩阵方程，其中 \( A \) 是一个系数矩阵，\( x \) 是未知向量，\( b \) 是常数向量。这类系统广泛出现在物理学、经济学和计算机科学中，例如电路分析、供需平衡或图像处理问题。解的存在性和唯一性取决于矩阵 \( A \) 的性质：当 \( A \) 可逆时，系统有唯一解 \( x = A^{-1}b \)；否则，可能有无穷多解或无解。

矩阵的逆定义为：若存在矩阵 \( B \) 使得 \( AB = BA = I \)（其中 \( I \) 是单位矩阵），则称 \( A \) 可逆，\( B \) 为 \( A \) 的逆矩阵，记为 \( A^{-1} \)。可逆矩阵必须是非奇异的（即行列式不为零），且其逆矩阵唯一。计算逆矩阵的方法包括高斯-约当消元法、伴随矩阵公式 \( A^{-1} = \frac{1}{\det(A)} \text{adj}(A) \)，以及利用分块矩阵技巧。这些方法不仅理论严谨，还在实际计算中高效可行，尤其适合处理大规模线性系统。

矩阵系统与逆的联系进一步体现在线性变换中。可逆矩阵对应可逆线性变换，这意味着变换可以无损反转，保持向量空间的结构不变。例如，在三维图形学中，逆矩阵常用于实现坐标系的逆变换，以恢复原始视角。逆矩阵在加密算法（如Hill密码）中扮演关键角色，通过可逆矩阵进行编码和解码，确保信息的安全性。

并非所有矩阵都可逆。奇异矩阵（行列式为零）代表线性相关系统，其逆不存在，这可能对应现实世界中的欠定或超定问题。例如，在数据拟合中，当观测点过多或过少时，线性回归模型可能无法得到唯一解，此时需借助广义逆（如Moore-Penrose伪逆）来寻找最佳近似解。这扩展了矩阵系统的应用范围，使其能处理更复杂的实际情况。

线性系统与矩阵的逆构成了矩阵系统的基石，它们通过简洁的数学形式揭示了变量间的深层关系。掌握这些概念，不仅有助于解决工程和科学中的具体问题，还为理解更高级的数学理论（如特征值分解和奇异值分解）奠定了坚实基础。在后续章节中，我们将继续探索矩阵系统在优化、动态模型等领域的扩展应用。