在推荐系统的演进历程中，协同过滤（Collaborative Filtering, CF）是奠定基础的经典方法。随着数据规模的爆炸式增长和业务场景的日益复杂，传统的协同过滤方法，如基于邻域的方法，逐渐显露出其局限性：难以处理大规模稀疏矩阵、无法有效利用丰富的辅助信息（如用户属性、物品特征、上下文等）。为了克服这些挑战，以矩阵分解（Matrix Factorization, MF）和因子分解机（Factorization Machines, FM）为代表的隐因子模型应运而生，它们不仅提升了推荐的精准度，也为推荐系统开启了从“用户-物品”二维交互迈向高阶特征组合分析的大门。

一、 矩阵分解：挖掘隐式偏好

矩阵分解的核心思想是将庞大的“用户-物品”评分矩阵（通常是高度稀疏的）分解为两个低维稠密矩阵的乘积。具体而言，假设我们有m个用户和n个物品，评分矩阵R (m×n)。矩阵分解旨在找到用户隐因子矩阵P (m×k)和物品隐因子矩阵Q (n×k)，使得它们的乘积近似于原始评分矩阵：R ≈ P * Q^T。

其中，k是隐因子的维度，通常远小于m和n。用户i对物品j的预测评分可以表示为：r̂{ij} = pi · qj^T，这里pi是P中代表用户i的k维隐向量，q_j是Q中代表物品j的k维隐向量。这些隐因子是模型自动学习得到的，它们可以解释为一些抽象的、可度量的“特征”，例如电影推荐中的“浪漫程度”、“动作成分”，或者音乐推荐中的“节奏感”、“流派偏向”。

矩阵分解的优势在于：

1. 解决稀疏性：通过将数据映射到低维空间，有效缓解了数据稀疏问题。
2. 可扩展性：模型参数数量为(m+n)k，远小于原始评分矩阵的mn，便于处理大规模数据。
3. 隐语义挖掘：能够自动发现用户和物品背后潜在的、未观测到的关联。

经典的矩阵分解模型（如FunkSVD）通过最小化预测评分与实际评分的均方误差来进行优化。在此基础上，加入偏置项（用户偏置、物品偏置和全局平均分）的偏置矩阵分解（Biased MF）以及考虑时间动态的时间敏感矩阵分解（TimeSVD++）等变体，进一步提升了模型的表达能力。

标准矩阵分解本质上仍是一个只利用“用户ID-物品ID”交互的模型。当面对丰富的特征信息（如用户 demographics、物品标签、浏览时间等）时，其建模能力就显得捉襟见肘。

二、 因子分解机：迈向高阶特征工程

因子分解机正是为了突破这一限制而设计的通用预测器。它不仅可以模拟矩阵分解（将用户ID和物品ID视为两个特征），更可以无缝地融入任意数量的实值特征，并对所有特征之间的交互进行建模。

FM模型的预测公式如下：
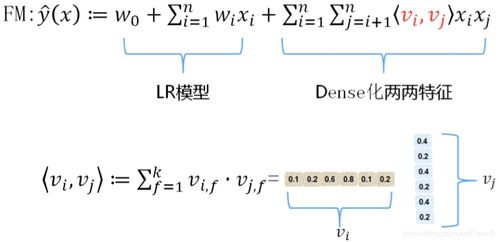
ŷ(x) = w0 + Σ{i=1}^{n} wi xi + Σ{i=1}^{n} Σ{j=i+1}^{n} ⟨vi, vj⟩ xi xj
其中：

• w_0是全局偏置。
• w_i建模特征i的一阶重要性（线性部分）。
• 核心部分是二阶交互项：⟨vi, vj⟩是特征i和特征j的隐向量vi和vj的点积，用于建模两个特征之间的交互效应。每个特征xi都关联一个k维隐向量vi。

FM的巧妙之处在于，它通过对交互参数进行矩阵分解（即假设交互参数矩阵W是低秩的），将交互参数的个数从O(n²)大幅降至O(n*k)，这使得FM即使在极度稀疏的数据下也能有效估计特征交互。

FM与MF的关系：如果将特征集仅设定为用户ID和物品ID的one-hot编码，那么FM的二阶交互部分就完全退化成了矩阵分解模型。因此，MF可以被视为FM在特定特征配置下的一个特例。FM是MF在特征维度上的泛化和扩展。

三、 矩阵分解系统与FM的实践与应用

在现代推荐系统架构中，矩阵分解和FM通常作为核心的召回（Recall）或排序（Ranking）模型嵌入其中。

1. 作为召回层：学习到的用户隐向量和物品隐向量可以用于高效的向量相似度计算（如余弦相似度）。通过近似最近邻搜索（ANN）技术，系统可以快速从海量物品库中检索出与用户兴趣最相关的数百个候选物品，送入后续的排序阶段。

1. 作为排序层：FM因其强大的特征组合能力，常被用作精细化的排序模型。它可以融合用户历史行为、物品属性、上下文信息（时间、地点、设备）、以及从其他渠道（如图像、文本）提取的深度特征，对所有特征进行二阶（甚至通过扩展实现更高阶）的交互建模，从而更精准地预测用户对某个候选物品的点击率（CTR）、转化率（CVR）或评分。

1. 系统实现：高效的实现对于工业级应用至关重要。FM模型的计算可以通过公式改写进行优化，使其计算复杂度线性于特征数量和非零特征数量。如今，FM及其衍生模型（如FFM, DeepFM）已被集成进诸多机器学习平台（如LibFM, xLearn, TensorFlow, PyTorch）。在分布式环境下，可以使用Spark MLlib或参数服务器架构进行大规模训练。

四、 与展望

从矩阵分解到因子分解机，代表了推荐算法从单纯的“协同”走向“特征融合”与“深度理解”的重要路径。MF以其简洁优雅的方式揭示了用户与物品间的潜在结构，而FM则提供了一个灵活的框架，将推荐问题转化为一个能够消化多源异构数据的标准预测任务。

尽管当前深度学习模型（如神经协同过滤NCF、 Wide & Deep、DeepFM）在推荐领域大放异彩，但MF和FM所蕴含的思想——低维嵌入、隐语义建模、稀疏特征下的高效交互——仍然是这些复杂模型的基石。理解矩阵分解和因子分解机，不仅是掌握经典推荐技术的钥匙，更是通往构建更智能、更个性化推荐系统道路上的坚实一步。未来的发展，将继续围绕如何更高效、更智能地融合与利用多模态、动态演化的数据，而MF与FM的精神内核，将持续在其中闪耀光芒。